Numeri periodici

Quando calcoliamo una frazione di questo tipo:

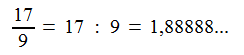
Otteniamo un numero decimale non limitato, questi numeri vengono chiamati numeri decimali illimitati, o più semplicemente numeri periodici.

La rappresentazione grafica che segue può essere utile per comprendere un numero periodico.

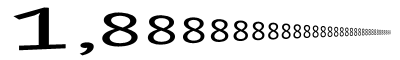
In questo caso la cifra 8 dopo la virgola si ripete all’infinito, è il periodo, e viene indicato di solito ponendo una linea continua sopra di esso (più sotto trovate “Come si scrivono” per approfondimento).

Definizione

Giunti a questo punto diamo una definizione di numero periodico (detto anche numero decimale illimitato).

Un numero decimale periodico è un numero razionale espresso come numero reale la cui parte decimale nella notazione si ripete indefinitamente.

Classificazione

I numeri periodici si dividono in:

• semplici: quando subito dopo la virgola è presente il periodo
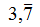
• misti: quando subito dopo la virgola sono presenti altre cifre prima del periodo (antiperiodo, lo vedremo dopo)

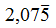
I numeri periodici sono caratterizzati da:

• parte intera: composta dalle cifre prima della virgola
• antiperiodo: composto da una o più cifre dopo la virgola, e prima del periodo
• periodo: composto da una o più cifre, che si ripetono all’infinito dopo la virgola

Ed ecco uno schema più chiaro.

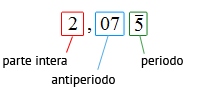
Ora che abbiamo parlato anche di numeri periodici misti, diamo la definizione:

Un numero decimale illimitato si dice periodico misto se in esso, fra la virgola e il periodo, esiste una cifra o un gruppo di cifre chiamato antiperiodo che non si ripete.

Come si scrivono

Per scrivere un numero periodico in forma compatta di solito si mette una linea continua sopra le cifre del periodo, oppure si racchiudono le cifre del periodo in una parentesi tonda. Esempio: 2,07(5)