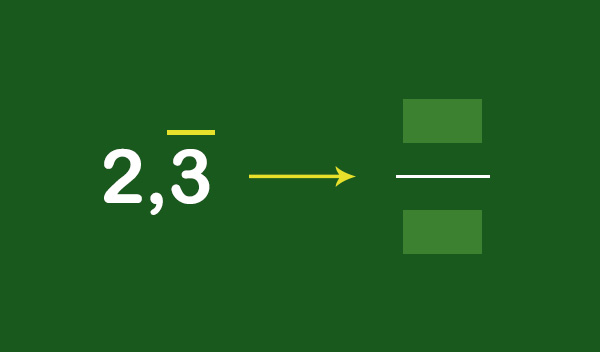Frazione generatrice di un numero periodico

La conoscenza dei numeri periodici è un prerequisito necessario, se non l’hai già fatto ti consigliamo ti consultare la nostra lezione sui numeri periodici.

Un numero periodico può essere trasformato in una frazione, detta frazione generatrice. Il risultato della frazione generatrice, ovvero la divisione tra numeratore e denominatore, è uguale al numero periodico di partenza.

Procedimento

La frazione generatrice di un numero periodico misto deve avere:

• A numeratore, la differenza tra il numero completo (scritto senza il periodo e senza la virgola) e tutto ciò che precede il periodo.
• A denominatore, tanti 9 quante sono le cifre che compongono il periodo e tanti 0 quante sono le cifre che compongono l’antiperiodo.

Schema

Possiamo seguire questo schema riassuntivo.

Esempi

Prendiamo in considerazione il seguente numero periodico

\[1,2\overline{57}\]

Il numero è così composto:

• 1257 è il numero completo, scritto senza periodo e virgola
• 57 è la parte periodica – detta anche periodo
• 2 è l’antiperiodo, ovvero la parte decimale che precede il periodo
• 12 è la parte del numero completo che precede il periodo

Scriviamo la frazione generatrice

\[\frac{1257-12}{?}\]

A numeratore scriviamo la differenza tra numero completo e tutto ciò che precede il periodo.

\[\frac{1257-12}{990} = \frac{1245}{990}\]

A denominatore scriviamo tanti 9 quante sono le cifre che compongono il periodo, seguiti da tanti 0 quante sono le cifre dell’antiperiodo.

A termine della lezione vi proponiamo altri esempi.

\[1,\overline{8}=\frac{18-1}{9}=\frac{17}{9}\] \[3,\overline{25}=\frac{325-3}{99}=\frac{322}{99}\] \[2,46\overline{3}=\frac{2463-246}{900}=\frac{2217}{900}\]